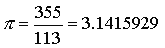Kako so računali Pi nekoč in kako ga računamo danes
Malo poznan verz iz Svetega Pisma pravi:
Nato je naredil ulito morje, od roba do roba široko deset komolcev, naokrog okroglo in pet
komolcev visoko. Trideset komolcev dolga vrvica ga je mogla okrog in okrog obseči.
(1. knjiga kraljev 7, 23)
Ta isti verz lahko najdemo v II Chronicles 4, 2. Pojavi se v načrtih za veliki Salomonov tempelj,
zgrajen okoli 950 pred našim štetjem (pr.n.š). Zanimiv je zato, ker lahko vidimo, da je število p
predstavljalo število 3 (kot se je izkazalo kasneje ta interpretacija p-ja ni bila čisto pravilna).
Seveda je to zelo nenatančna vrednost za tisti čas, saj so že veliko pred tem zasledili Egipčanski
in Mezopotamski p, ki sta bila 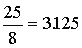 in
in 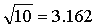 .
.
Seveda pa je šlo tu za zelo velik srebrn (oz. medeninast) odlitek, pri katerem je bilo zelo težko
doseči visoko natančnost v geometriji oz. te natančnosti sploh niso potrebovali.
Kasneje so proučevali ta načrt in ugotovili sledeče:
Ta odlitek je imel debele stranice in meritev premera 10 komolcev se je nanašala na
zunanji premer, medtem ko se je meritev obsega 30 komolcev nanašala na notranji obseg.
Debelina obroča je bila izmerjena v »dlaneh«, kar je približno 4 inče. In če uporabimo
približek 17.75 za komolec, potem je vrednost p v enačbi

enaka 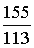 = 3.14159292.
= 3.14159292.
Dejstvo, da je razmerje med obsegom in premerom kroga konstanta, je znano že zelo dolgo.
Zgodnje vrednosti števila p, kot je npr. Svetopisemski  ,
so bile dobljene z meritvami. Na Egipčanskem Rhindovem papirusu (1650 pr.n.š) je jasno
razvidno, da je število
,
so bile dobljene z meritvami. Na Egipčanskem Rhindovem papirusu (1650 pr.n.š) je jasno
razvidno, da je število  enako
enako 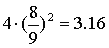 .
Prvi teoretični izračuni so bili po sedaj znanih dejstvih delo Arhimeda iz Syrakuse (287-212 pr.n.š).
Dobil je sledečo aproksimacijo:
.
Prvi teoretični izračuni so bili po sedaj znanih dejstvih delo Arhimeda iz Syrakuse (287-212 pr.n.š).
Dobil je sledečo aproksimacijo:
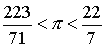 Poseben povdarek velja tu na neenakostih. Arhimed
je vedel, kar mnogi do tedaj niso:
vedel je da
Poseben povdarek velja tu na neenakostih. Arhimed
je vedel, kar mnogi do tedaj niso:
vedel je da  ni enak
ni enak  .
Če vzamemo za najboljši približek kar aritmetično sredino obeh meja dobimo: 3.1218.
.
Če vzamemo za najboljši približek kar aritmetično sredino obeh meja dobimo: 3.1218.
Arhimedov argument je sledeč:
Imejmo krog z radijem 1, v katerega včrtamo pravilen večkotnik z ogljišči, ki ima polobseg
bn in očrtamo pravilen večkotnik prav tako z ogljišči, ki ima polobseg an.
Skica za n = 2 je na desni:
 Tako dobimo naraščajoče zaporedje:
Tako dobimo naraščajoče zaporedje:
b1, b2, b3, ...
in padajoče zaporedje:
a1, a2, a3, ...
in oba zaporedja imata limito  .
.
Če uporabimo trigonometrični zapis , vidimo da sta oba polobsega podana z:
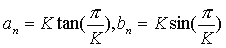
kjer je K =  . Enako je
. Enako je
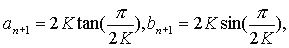
in ni težko videti, da je

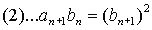
Arhimed je začel z 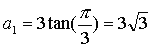 in
in  .
Nato je s pomočjo (1) in (2) izračunal a6 in b6.
Njegovi izračuni so dali iskano neenakost:
.
Nato je s pomočjo (1) in (2) izračunal a6 in b6.
Njegovi izračuni so dali iskano neenakost:
 Tu je pomembno, da je uporaba trigonometrije »nezgodovinska«, saj Arhimed ni poznal
algebraičnega in trigonometričnega zapisa. (1) in (2) je opisal čisto geometrijsko.
Prav tako ni poznal današnjega decimalnea zapisa, tako da izračun a6 in
b6 ni bil trivialen račun. Zato je njegova predstavitev in izračuni zares čudovito
delo. Čudovito pri tem ni to, da se je ustavil šele pri 96-kotnikih ampak že to, da je sploh šel
tako daleč.
Tu je pomembno, da je uporaba trigonometrije »nezgodovinska«, saj Arhimed ni poznal
algebraičnega in trigonometričnega zapisa. (1) in (2) je opisal čisto geometrijsko.
Prav tako ni poznal današnjega decimalnea zapisa, tako da izračun a6 in
b6 ni bil trivialen račun. Zato je njegova predstavitev in izračuni zares čudovito
delo. Čudovito pri tem ni to, da se je ustavil šele pri 96-kotnikih ampak že to, da je sploh šel
tako daleč.
Nekateri pa so šli celo še dlje:
Ptolemej (cca. 150) 3.1416
Tsu Ch'ung Chi (430-501) 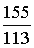 Al-Khwarizmi (cca. 800) 3.1416
Al-Kashi (cca. 1430) na 14 mest
Viete (1540-1603) na 9 mest
Roomen (1561-1615) na 17 mest
Van Ceulen (cca. 1600) na 35 mest
Razen Tsu Ch'ung Chi ni nihče vedel o Arhimedovem delu, zato ni bilo s teoretičnega vidika
narejen noben korak naprej, le natančnost računanja se je povečevala.
Al-Khwarizmi je živel v Bagdadu. Je »oče« algebre. V naslovu ene izmed njegovih knjig je
beseda »al jabar« iz katere izvira tudi današnji pojem »algebra«. Nekateri menijo, da iz
njegovega imena izvira tudi beseda »algoritmi«.
Al-Khwarizmi (cca. 800) 3.1416
Al-Kashi (cca. 1430) na 14 mest
Viete (1540-1603) na 9 mest
Roomen (1561-1615) na 17 mest
Van Ceulen (cca. 1600) na 35 mest
Razen Tsu Ch'ung Chi ni nihče vedel o Arhimedovem delu, zato ni bilo s teoretičnega vidika
narejen noben korak naprej, le natančnost računanja se je povečevala.
Al-Khwarizmi je živel v Bagdadu. Je »oče« algebre. V naslovu ene izmed njegovih knjig je
beseda »al jabar« iz katere izvira tudi današnji pojem »algebra«. Nekateri menijo, da iz
njegovega imena izvira tudi beseda »algoritmi«.
Evropska renesansa je prinesla nov zagon tudi na matematičnem področju. Posledično iz
tega časa izvirajo tudi prve formule za izračun števila Pi. Eno prvih je objavil Wallis
(1616-1703):
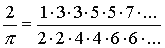 Najbolja znana iz tistega časa pa se glasi:
Najbolja znana iz tistega časa pa se glasi:

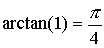 To formulo nekateri pripisujejo Leibniz-u (1646-1716), vendar spet drugi menijo, da jo je prvi
odkril James Gregory (1638-1675). V teh dveh formulah je tudi odgovor vsem skeptikom,
ki se nikakor niso hoteli sprijazniti z neskončnostjo. Tu se lepo vidi, da lahko tudi neskončen
proces (vsota) da zelo uporaben rezultat.
To formulo nekateri pripisujejo Leibniz-u (1646-1716), vendar spet drugi menijo, da jo je prvi
odkril James Gregory (1638-1675). V teh dveh formulah je tudi odgovor vsem skeptikom,
ki se nikakor niso hoteli sprijazniti z neskončnostjo. Tu se lepo vidi, da lahko tudi neskončen
proces (vsota) da zelo uporaben rezultat.
V Gregory-jevi vsoti bi morali sešteti približno 10000 členov te vsote, da bi dobili natančnost
na 4 decimalna mesta (napaka bi morala biti manjša kot 0.00005 = 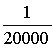 ). Gregory ni pokazal le
pravilnost zgornje formule. Pokazal je še bolj splošno:
). Gregory ni pokazal le
pravilnost zgornje formule. Pokazal je še bolj splošno:
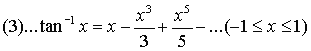 Če vstavimo x=1 dobimo ravno Gregory-jevo vsoto.
Upoštevajmo sedaj še dejstvo, da je
Če vstavimo x=1 dobimo ravno Gregory-jevo vsoto.
Upoštevajmo sedaj še dejstvo, da je
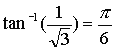 Iz tega sledi:
Iz tega sledi:
 Ta formula pa konvergira občutno hitreje. 10. člen je
Ta formula pa konvergira občutno hitreje. 10. člen je 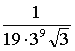 kar je manj kot 0.00005 in zato imamo vsaj 4 mesta natančno po samo 9. iteraciji.
kar je manj kot 0.00005 in zato imamo vsaj 4 mesta natančno po samo 9. iteraciji.
Še boljša ideja pa je če vzamemo formulo:
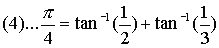 Za izračun števila Pi potem izračunamo dve vsoti (3) z
Za izračun števila Pi potem izračunamo dve vsoti (3) z 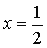 in
in 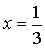 .
.
Še boljšo konvergenco pa lahko dobimo, če najdemo taki dve števili a in b, čim večji, da bo
veljalo:
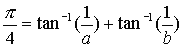 Leta 1706 je Machin našel takšno formulo:
Leta 1706 je Machin našel takšno formulo:
 To formulo ni težko dokazati, če znamo dokazati (4).
To formulo ni težko dokazati, če znamo dokazati (4).
S tako formulo je edina težava pri računanju števila Pi le »dolgčas« pri računaju.
Našli so se tudi taki, ki so bili dovolj trmasti in so si vzeli veliko časa in truda in izračunali
Pi že zelo natančno.
Med njimi je bil tudi Shaks, ki je uporabil Machin-ovo formulo s pomočjo katere je izračunal
Pi na 707 mest, vendar je na žalost napravil napako, tako da vsa mesta niso bila pravilna.
Pa si poglejmo kratek pregled napredovanja:
1699 Sharp je uporabil Gregoryjevo formulo, da je dobil pravilnih 71 mest
1701 Machin je uporabil izboljšano Gregoryjevo formulo in dobil 100 pravilnih mest
1719 De Lagny je naračunal kar 112 pravilnih mest
1789 Vega, najprej na 126 mest, leta 1794 pa na 136 mest
1841 Rutherford na 152 mest, leta 1853 pa na kar 440
1873 Shanks je bil prepričan, da jih je pravilno izračunal 707, vendar se je kasneje izkazalo, da jih je imel prav samo 527.
Shanks je vedel, da je Pi iracionalno število. To je dokazal že Lambert leta 1761. Kmalu za
tem ko je Shanks objavil svoje izračune je Lindemann pokazal, da je Pi transcendentno število.
Torej Pi ni rešitev nobene polinomske enačbe s celimi koeficienti. Posledica tega pa je, da je
kvadratura kroga nemogoča. Transcendentnost Pi-ja implicira, da ne obstaja pravilo s
pomočjo katerega, bi lahko konstruirali kvadrat, ki bi bil po ploščini enak danemu krogu.
V času, ko je Shanks objavil svoje rezultate je živel tudi De Morgan. Nekateri so mu rekli kar
statistični »freak«. V Shanksovem izračunu je opazila, da »kronično« primanjkuje sedmic.
To je omenil v »Budget of Paradoxes« leta 1872. Šele leta 1945 je Ferguson odkril, da je
Shanks napravil napako na 528 mestu, kar je imelo za posledico, da so bile vse nadaljne
številke napačne.
V tem času pa so začeli prodirati na to področje tudi računalniki. Tako so leta 1949 s
pomočjo računalnika izračunali Pi na 2000 mest natančno. V tem izračunu, pa je bilo število
sedmic v skladu s pričakovanji De Morgana.
Spodobilo bi se nekaj reči tudi o razvoju notacije števila Pi kot  .
.
Leta 1647 je Oughtred uporabil zapis 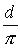 za razmerje med
premerom in obsegom kroga. Davi Gregory (1697) je uporabljal oznako
za razmerje med
premerom in obsegom kroga. Davi Gregory (1697) je uporabljal oznako  za razmerje med obsegom kroga in njegovim polmerom. Prvi, ki je uporabljal notacijo
za razmerje med obsegom kroga in njegovim polmerom. Prvi, ki je uporabljal notacijo  kot samostojno pa je bil William Jones (1706, Wels), ki je zapisal
kot samostojno pa je bil William Jones (1706, Wels), ki je zapisal  .
Leta 1737, ga je privzel v svojih zapisih Euler in kmalu je postal standardna notacija za Pi.
.
Leta 1737, ga je privzel v svojih zapisih Euler in kmalu je postal standardna notacija za Pi.
Zanimiv je tudi naslednji primer računanja števila Pi:
Imenuje se Buffon-ov eksperiment s šivanko. Imejmo pravilno mrežo vzporednih premic.
Medsebojna oddaljenost je 1. Na to mrežo potem mečemo šivanko dolžine k < 1. Verjetnost,
da bo šivanka padla čez premico je  .
Kar nekaj ljudi je poizkušalo izračunati Pi z metanjem šivanke. Med njimi je bil tudi Lazzerini
(1901), ki je naredil 34080 metov in dobil:
.
Kar nekaj ljudi je poizkušalo izračunati Pi z metanjem šivanke. Med njimi je bil tudi Lazzerini
(1901), ki je naredil 34080 metov in dobil:
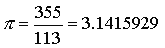 Prav tako število je, zanimivo, dobil tudi Tsu Ch'ung Chi. Ta rezultat je sumljivo dober.
Tudi število metov (34080) je »čudno«. Kendall in Moran sta komentirala, da je mogoče
dobiti dober rezultat če prekineš eksperiment pri optimalnem številu metov. Vendar je to
kljub temu zelo nenatančno računanje. Kendall in Moran sta potem komentirala, da bi bilo
bolje, če bi odrezal velik kos lesa v obliki kroga in mu izmeril obseg in premer in s tem
izračunal Pi.
Prav tako število je, zanimivo, dobil tudi Tsu Ch'ung Chi. Ta rezultat je sumljivo dober.
Tudi število metov (34080) je »čudno«. Kendall in Moran sta komentirala, da je mogoče
dobiti dober rezultat če prekineš eksperiment pri optimalnem številu metov. Vendar je to
kljub temu zelo nenatančno računanje. Kendall in Moran sta potem komentirala, da bi bilo
bolje, če bi odrezal velik kos lesa v obliki kroga in mu izmeril obseg in premer in s tem
izračunal Pi.
Odprta vprašanja:
Ali se vska od številk 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 pojavi v Pi-ju neskončnokrat?
Brouwerjevo vprašanje: Ali je v decimalnem zapisu števila Pi 1000 zaporednih mest enih 0?
Ali se v številu Pi enako pogosto pojavljajo števke (asimptotsko)?
...
Fibonaccijeva števila in Pi


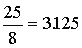 in
in 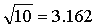 .
.

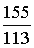 = 3.14159292.
= 3.14159292. ,
so bile dobljene z meritvami. Na Egipčanskem Rhindovem papirusu (1650 pr.n.š) je jasno
razvidno, da je število
,
so bile dobljene z meritvami. Na Egipčanskem Rhindovem papirusu (1650 pr.n.š) je jasno
razvidno, da je število  enako
enako 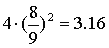 .
Prvi teoretični izračuni so bili po sedaj znanih dejstvih delo Arhimeda iz Syrakuse (287-212 pr.n.š).
Dobil je sledečo aproksimacijo:
.
Prvi teoretični izračuni so bili po sedaj znanih dejstvih delo Arhimeda iz Syrakuse (287-212 pr.n.š).
Dobil je sledečo aproksimacijo: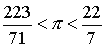
 ni enak
ni enak  .
Če vzamemo za najboljši približek kar aritmetično sredino obeh meja dobimo: 3.1218.
.
Če vzamemo za najboljši približek kar aritmetično sredino obeh meja dobimo: 3.1218. Tako dobimo naraščajoče zaporedje:
Tako dobimo naraščajoče zaporedje: .
.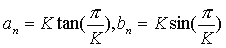
 . Enako je
. Enako je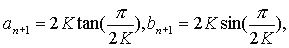

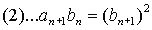
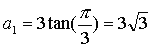 in
in  .
Nato je s pomočjo (1) in (2) izračunal a6 in b6.
Njegovi izračuni so dali iskano neenakost:
.
Nato je s pomočjo (1) in (2) izračunal a6 in b6.
Njegovi izračuni so dali iskano neenakost:
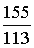
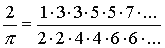

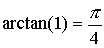
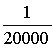 ). Gregory ni pokazal le
pravilnost zgornje formule. Pokazal je še bolj splošno:
). Gregory ni pokazal le
pravilnost zgornje formule. Pokazal je še bolj splošno: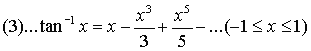
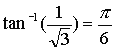

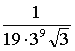 kar je manj kot 0.00005 in zato imamo vsaj 4 mesta natančno po samo 9. iteraciji.
kar je manj kot 0.00005 in zato imamo vsaj 4 mesta natančno po samo 9. iteraciji. 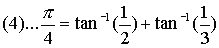
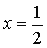 in
in 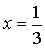 .
. 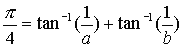

 .
.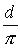 za razmerje med
premerom in obsegom kroga. Davi Gregory (1697) je uporabljal oznako
za razmerje med
premerom in obsegom kroga. Davi Gregory (1697) je uporabljal oznako  za razmerje med obsegom kroga in njegovim polmerom. Prvi, ki je uporabljal notacijo
za razmerje med obsegom kroga in njegovim polmerom. Prvi, ki je uporabljal notacijo  kot samostojno pa je bil William Jones (1706, Wels), ki je zapisal
kot samostojno pa je bil William Jones (1706, Wels), ki je zapisal  .
Leta 1737, ga je privzel v svojih zapisih Euler in kmalu je postal standardna notacija za Pi.
.
Leta 1737, ga je privzel v svojih zapisih Euler in kmalu je postal standardna notacija za Pi.
 .
Kar nekaj ljudi je poizkušalo izračunati Pi z metanjem šivanke. Med njimi je bil tudi Lazzerini
(1901), ki je naredil 34080 metov in dobil:
.
Kar nekaj ljudi je poizkušalo izračunati Pi z metanjem šivanke. Med njimi je bil tudi Lazzerini
(1901), ki je naredil 34080 metov in dobil: