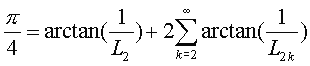Spomnimo se kaj so fibonaccijeva števila:
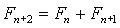
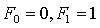
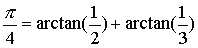
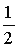 in
in
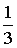 oba manjša od 1. Manjša vrednost argumentov pomeni
boljšo konvergenco vsote in zato lahko izračunamo Pi zelo natancno v nekem doglednem času.
Na tem mestu se vprašamo: Ali obstajata še kakšna dva kota, katerega tangens poznamo in
katerih rezultat je
oba manjša od 1. Manjša vrednost argumentov pomeni
boljšo konvergenco vsote in zato lahko izračunamo Pi zelo natancno v nekem doglednem času.
Na tem mestu se vprašamo: Ali obstajata še kakšna dva kota, katerega tangens poznamo in
katerih rezultat je 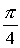 .Odgovor je seveda DA. Pa si poglejmo
nekaj primerov:
.Odgovor je seveda DA. Pa si poglejmo
nekaj primerov:Poizkusimo postaviti bolj splošno formulo: Pravkar smo videli, da imamo neskončno mnogo formul za izračuna števila Pi, ki uporabljajo fibonaccijeva števila:


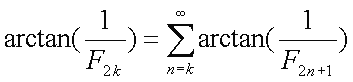
Lucasova števila in Pi
Lucasova števila (oznaka: Ln)se računa po enakem postopku kot fibonacciejva. Edina razlika
je v tem, da začnemo z 2 in 1 in ne z 0 in 1. V tabeli je nekaj členov za primerjavo:
| n: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
| Fn: | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | ... |
| Ln: | 2 | 1 | 3 | 4 | 7 | 11 | 18 | 29 | 47 | 76 | 123 | ... |

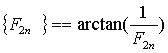 ) ob bok Eulerjevi formuli (A) dobimo:
) ob bok Eulerjevi formuli (A) dobimo:{F2n+1} = {L2n} + {L2n+2} (B)
Poglejmo si to na primeru: Začnimo z {1} = {2} + {3}={F3} + {F4} Sedaj lahko liho indeksirano »Fibonaccijevo število« nadomestimo z uporabo (B) z vsoto dveh Lucasovih števil. Tako dobimo:
Ko naletimo na sodo indeksirano »fibonaccijevo število« ga z uporabo (A) nadomestimo z vsoto dveh fibonaccijevih števil. Dobimo:
Tako dobimo sledečo formulo: