(z vidika statistike)

Statistika je veda, ki preučuje množične pojave. Z zbiranjem, urejanjem, grupiranjem, povezovanjem, prikazovanjem in analiziranjem številskih podatkov o teh pojavih skuša odkriti njihove splošne zakonitosti in nato pridobljena spoznanja izkoristiti za oblikovanje ustreznih napovedi oziroma odločitev. Skupna značilnost večine statističnih proučevanj je, da pojavov ne moremo zajeti v celoti (so preobsežni, iz ekonomskega vidika je prezahtevno,...). Prisiljeni smo sklepati na osnovi nepopolnih informacij, dobljenih na vzorčnih populacijah, zato tudi o dobljenih ugotovitvah ne moremo trditi, da so zagotvo pravilne, lahko so le bolj ali manj verjetne. Za pravilno razumevanje dejanske vrednosti oziroma zanesljivosti podatkov moramo zato obvladati vsaj osnove verjetnostnega računa.
Dobljene podatke (niz vrednosti statističnega znaka) običajno grupiramo, da se izognemo nepreglednosti. Tako dobljene frekvence podatkov predstavimo v tabelah ali na grafu v obliki histograma ali poligona.
V tem članku se bomo ukvarjali s porazdelitvami dobljenih podatkov, natančneje, z normalno porazdelitvijo, za razumevanje je nujno potrebno poznavanje osnovnih pojmov statistike in verjetnostnega računa.
2.NORMALNA PORAZDELITEV
Vemo, da je verjetnostna porazdelitev vrednosti znakov različnih populacij različna, kljub tej različnosti se mnogo pojavov porazdeljuje podobno. Med takimi teoretičnimi porazdelitvami je najpomembnejša normalna porazdelitev, mnoge druge porazdelitve se ji v posebnih pogojih približujejo.
Matematično normalno porazdelitev izpeljemo iz binomske porazdelitve Bin(n,p), ta ima zanimivo lastnost, da pri povečevanju parametra n (velikosti vzorca) graf ustrezne verjetnostne porazdelitve postaja vedno bolj podoben gladki krivulji zvončaste oblike (primer večanja parametra). Približevanje binomske porazdelitve si lahko ogledate tudi z programom v Javi. Krivuljo binomske porazdelitve pri velikem n lahko opišemo z enačbo, ki predstavlja verjetnostno gostoto normalno porazdeljene slučajne spremenljivke:
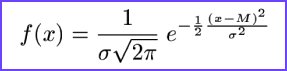
Formula normalne porazdelitve
Tako krivuljo imenujemo normalna ali Gaussova krivulja po nemškem matematiku Carlu Friedrichu Gaussu (1777 - 1855) , ki jo je uporabil v analizi slučajnih napak pri merjenjih. Večkrat uporabljano ime normalna krivulja izvira iz dejstva, da z njo lepo opišemo porazdelitev frekvenc izmerkov pri zaporednih merjenjih neke količine v normalnih pogojih, torej takrat, ko pri merjenju ne delamo sistematičnih napak, ampak so napake povsem slučajne. Izmerki so vrednosti neke slučajne spremenljivke X (zato tudi f ( x ) matematiki imenujejo verjetnostna gostota) in lahko zavzamejo katerokoli realno vrednost in ne le celoštevilske, zato imamo opraviti z zvezno slučajno spremenljivko (zvezno porazdeljenim znakom), normalno porazdelitev pa štejemo med zvezne porazdelitve.
Lep primer normalne porazdelitve je tudi naključno padanje kroglic:
Oglejmo si sedaj graf neke normalne porazdelitve (na absciso nanašamo vrednost znaka in na ordinato ustrezne verjetnostne gostote):
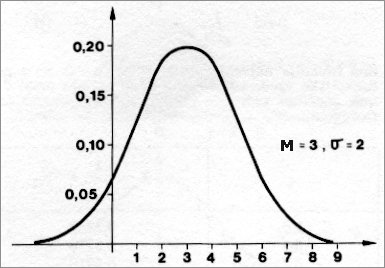
Graf normalne porazdeljene slučajne spremenljivke
Krivulja ima, kot smo že povedali, obliko simetričnega zvonca in je unimodalna (ima en vrh). Površina pod krivuljo je, zaradi korena v imenovalcu enačbe, enaka 1 in pomeni verjetnost, da ima lahko slučajna spremenljivka (znak) katerokoli vrednost. V enačbi krivulje nastopata dva parametra:
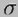 : standardni odklon (standardna deviacija)
: standardni odklon (standardna deviacija)
- M : matematično upanje (aritmetična sredina)
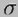 :
:
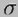 )
)
Ta dva parametra vplivata na graf krivulje. Aritmetična sredina (matematično upanje)
M
odloča o položaju
krivulje na abscisni osi - največjo vrednost ![]() dobimo
pri x = M (največja verjetnostna gostota oz. vrh krivulje!).
Standardni odklon meri razpršenost vrednosti okoli matematičnega upanja (oz.
aritmetične sredine), zato vpliva na sploščenost krivulje (večji kot je odklon,
bolj sploščena je krivulja)
.
dobimo
pri x = M (največja verjetnostna gostota oz. vrh krivulje!).
Standardni odklon meri razpršenost vrednosti okoli matematičnega upanja (oz.
aritmetične sredine), zato vpliva na sploščenost krivulje (večji kot je odklon,
bolj sploščena je krivulja)
.
Ko smo zapisali, da največja verjetnostna gostota nastopi pri aritmetični sredini, smo s tem povedali tudi, da je pri normalni porazdelitvi Modus enak Aritmetični sredini, zaradi simetričnosti pa je tema dvema enaka tudi Medijana. Vrednosti levo in desno (navzgor in navzdol) od aritmetične sredina imajo vse manjšo verjetnostno gostoto. Z zbiranjem, urejanjem in analiziranjem podatkov različnih normalno porazdeljenih znakov so ugotovili, da se vse tako porazdeljene slučajne spremenljivke porazdeljujejo podobno - na določen interval pade enak procent vrednosti te spremenljivke!
| INTERVAL % VREDNOSTI |
|---|
( M - 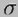 , M + , M + 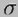 )
68,27% )
68,27%
|
( M - 2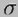 , M + 2 , M + 2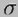 )
95,45% )
95,45%
|
( M - 3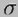 , M + 3 , M + 3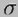 )
99,73% )
99,73%
|
Iz zgornje tabele je razvidno, da se za več kot tri standardne odklone od aritmetične sredine razlikuje le 0.27% vseh zbranih podatkov. S tem dejstvom si lahko pomagamo pri računanju verjetnosti, da bo imela slučajna spremenljivka določeno vrednost. Na grafu verjetnost dogodka predstavlja ploščina pod normalno krivuljo. Tako lahko izračunamo verjetnost:
- da bo imela spremenljivka vrednost večjo od določene vrednosti
- da bo imela vrednost manjšo od določene vrednosti
- da bo imela vrednost na nekem danem intervalu
Če bi vsako stvar računali matematično pravilno, s pomočjo integrala verjetnostne gostote na nekem intervalu, bi nas verjetno že pri prvem računu zagrabila panika. Vemo tudi, da so si normalne porazdelitve različne in zato težko primerljive med seboj. Primerjanje in računanje si močno olajšamo z standardiziranjem, ki nam bo poenotilo vse normalne porazdelitve!
3. STANDARDIZIRANA NORMALNA PORAZDELITEV
Kljub temu, da se pojavi normalno distribuirajo, so njihove normalne krivulje postavljene na različnih
mestih na abscisni osi in so bolj ali manj sploščene. Te razlike med krivuljami odpravimo
z standardiziranjem odklonov
vrednosti spremenljivke od aritmetične sredine. Standardiziran odklon
označimo z Z, dobimo ga iz slučajne spremenljivke X, tako da ji odštejemo
aritmetično sredino M in dobljeno
delimo z njenim standardnim odklonom 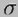 :
:

Standardizirana spremenljivka X
Tako dobljene spremenljivka je še vedno porazdeljena normalno:
le njena enačba se poenostavi:
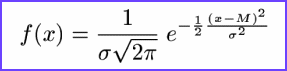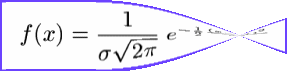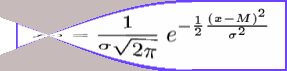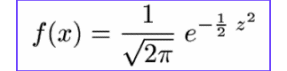
Formula standardizirane normalne porazdelitve
in jo imenujemo Standardizirana normalna porazdelitev. Aritmetična sredina je sedaj pri vrednosti 0, standardni odklon pa je enak 1. Tako, preprostejšo funkcijo lažje proučimo in primerjamo z krivuljami ostalih normalno porazdeljenih spremnljivk.
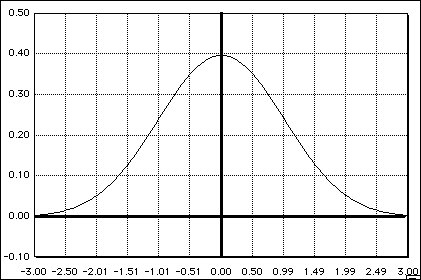
Graf standardizirane normalne porazdelitve
Površina pod standardizirano normalno krivuljo je 1, deli površin pa predstavljajo verjetnost, da bo slučajna spremenljivke (statistični znak) Z zavzela določeno vrednost. Površine pod krivuljo so statistiki tabelirali na štiri decimalke natančno. S pomočjo tabel lahko hitro izračunamo verjetnost, da spremenljivka zavzame določeno vrednost, oziroma, da njene vrednosti ležijo na določenem intervalu. Manjša pomankljivost je, da so tabelirane le površine desno od 0, vendar nam to ne bi smelo povzročati prevelikih preglavic, saj vemo, da je normalna krivulja zvončaste oblike in zato - simetrična. Torej, če nas zanima ploščina na negativnem delu v tabeli poiščemo procente za ekvivalentno ploščino desno od aritmetične sredine. Podobno se lotimo problema iskanje verjetnosti na določenem intervalu - odštejemo ali seštejemo verjetnosti dveh intervalov.
Da ne bomo samo teoretizirali si raje oglejmo nekaj primerov:
-
Primer 1:
Za standardizirano normalno porazdeljeno slučajno spremenljivko (statistični znak) določi verjetnost, da zavzame poljubno
vrednost z intervala [ 0 , 2 ].
Rešitev: Iščemo verjetnost da slučajna spremenljivka zavzame vrednost med aritmetično sredino 0 (standardizirana je!) in vrednostjo 2. Te vrednosti imamo zapisane v tabeli - preostane nam le še, da najdemo zapis v tabeli, ki nam pove iskani procent verjetnosti (s P označimo verjetnost dogodka):P (0 < X < 2)= f (2) = 0,4772 Kar pomeni, da je naša iskana verjetnost 47,72%.
-
Primer 2:
Za standardizirano normalno porazdeljeno slučajno spremenljivko (statistični znak), določi verjetnost, da zavzame
poljubno vrednost, manjšo od 2.
Rešitev: Ker iščemo vrednost manjšo od 2 lahko s pomočjo grafa ugotovimo, da je to skupna verjetnost dveh delov ploščin pod krivuljo - ploščine levo od aritmetične sredine (tu bomo upoštevali, da je v odmiku 3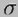 levo od
aritmetične sredine 49,865%
vse populacije, torej skoraj 50%)in ploščine na intervalu [0,2].
Z enačbo to lahko zapišemo kot:
levo od
aritmetične sredine 49,865%
vse populacije, torej skoraj 50%)in ploščine na intervalu [0,2].
Z enačbo to lahko zapišemo kot:
P (X < 2)= P (X < 0) + P (0 < X < 2) = f (4) + f (2) = 0,5 + 0,4772 = 0,9772 Kar pomeni, da je naša iskana verjetnost 97,72%.
-
Primer 3:
Za standardizirano normalno porazdeljeno slučajno spremenljivko določi verjetnost, da zavzame poljubno
vrednost z intervala [ 1 , 2 ].
Rešitev: Iščemo verjetnost da slučajna spremenljivka zavzame vrednost med 1 in 2. Vrednosti za verjetnosti od aitmetične sredine do vsake vrednosti posebaj imamo zapisane v tabeli - preostane nam le, da najdemo zapisa najdemo v tabeli in ju odštejemo (če ne veš zakaj, si oglej sliko graf normalne krivulje in se spomni kako se izračuna ploščina na nekem intervalu pod krivuljo!)P (1<=X<=2)= f (2) - f (1) = 0,4772 - 0,3413 = 0,1359 Kar pomeni, da je naša iskana verjetnost 13,59%.
-
Primer 4:
Za standardizirano normalno porazdeljeno slučajno spremenljivko določi verjetnost, da zavzame poljubno
vrednost z intervala [ -1 , 2 ].
Rešitev: Iščemo verjetnost da slučajna spremenljivka zavzame vrednost med -1 in 2. Verjetnost spet razdelimo na dva dela: [-1,0) in [0,2]. Tu se bodo verjetnosti obeh delov seštele:P (-1<=X<=2) = f (1) + f (2) = 0,3413 + 0,4772 = 0,8185 Kar pomeni, da je naša iskana verjetnost 81,85%.
Vsi primeri so bili narejeni za standardizrane slučajne spremenljivke, če se v nalogah znajdejo nestandardizirane slučajne spremenljivke, je dela le toliko več, kolikor ga porabimo za standardiziranje!
-
Primer 5:
Za normalno porazdeljeno slučajno spremenljivko (njeno povprečje
je 100, standardni odklon 10) določi verjetnost, da zavzame poljubno
vrednost med 90 in 120.
Rešitev: Iščemo verjetnost da slučajna spremenljivka zavzame vrednost med 90 in 120. Verjetnosti znamo računati za standardizirane spremenljivke, zato ti dve vrednosti najprej standardiziram. Če 90 odštejem M = 100 in ga nato delim z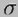 = 10, dobimo prvo standardizirano
vrednost: Z ( 90 ) = -1. Podobno dobimo Z ( 120 ) = 2.
Iščemo torej verjetnost, da standardizirana normalna spremenljivka zavzame vrednosti
na intervalu [ -1 , 2 ]. Tako naša naloga postane enaka Nalogi 4 in
zato je rešitev
= 10, dobimo prvo standardizirano
vrednost: Z ( 90 ) = -1. Podobno dobimo Z ( 120 ) = 2.
Iščemo torej verjetnost, da standardizirana normalna spremenljivka zavzame vrednosti
na intervalu [ -1 , 2 ]. Tako naša naloga postane enaka Nalogi 4 in
zato je rešitev P (-1<=X<=2) = f (1) + f (2) = 0,3413 + 0,4772 = 0,8185 Kar pomeni, da je naša iskana verjetnost 81,85%.
Za najbolj lene med bralci, pa je v naslednjem poglavju kuharski recept za reševanje nalog.
3. UPORABA
-
Kako izračunati verjetnost (v procentih), da bo normalno porazdeljena
slučajna spremenljivka zavzela določeno vrednost?
- določite slučajno spremenljivko (statistični znak)
- določite njeno povprečno vrednost (aritmetično sredino) in njen standardni odklon iz podatkov
- ugotovite kakšna verjetnost vas zanima: določena vrednost ali interval
- standardizirajte spremenljivko (za vse dane podatke!)
- poiščite verjetnosti v tabeli verjetnosti
Pri izračunu površine pod normalno krivuljo pa si lahko pomagamo tudi s programom v Javi!
- NALOGA 1( REŠITEV ):
Za slučajno spremenljivko s standardizirano normalno porazdelitvijo
izračunaj:
- verjetnost P ( X > 1 )
- verjetnost P ( -1 < X < 0,5 )
- verjetnost P ( X < - 0,2 )
- NALOGA 2( REŠITEV ): Za
normalno porazdeljeno slučajno spremenljivko s povprečno vrednostjo M = 10
in standardnim odklonom
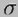 = 9 izračunaj:
= 9 izračunaj:
- verjetnost P ( X > 8 )
- verjetnost P ( 8 < X < 12 )
- verjetnost P ( X < 6 )
- NALOGA 3( REŠITEV ): Izdelek je prvorazreden, če se ne razlikuje od nominalnega za več
kot 3,40cm. Slučajni odkloni izdelkov od nominalnega so normalno
porazdeljeni s povprečno vrednostjo 0 in standardnim odklonom
3cm. Koliko procentov proizvodnje je prvorazredne?
- NALOGA 4( REŠITEV
): Življenska doba žarnic je slučajna spremenljivka, porazdeljena
normalno z standardnim odklonom 50 okoli povprečne življenske
dobe 1000 ur. Izračunaj verjetnost, da žarnica zdrži vsaj
1050 ur.
- NALOGA 5( REŠITEV ): Za slučajno spremenljivko porazdeljeno normalno okoli srednje
vrednosti 0, z standardnim odklonom 1 izračunaj naslednje
verjetnosti dogodkov:
- da zavzame vrednost, večjo od 0,8
- da zavzame vrednost, manjšo od 1,5
- da zavzame vrednost, večjo od - 1
- da zavzame vrednost, manjšo od 0,5
- da zavzame vrednost, manjšo od - 0,4
- da zavzame vrednost z intervala [0,7 , 1,5]
- da zavzame vrednost z intervala [- 1 , 1,5]
Povzeto po knjigah:
- MATEMATIKA (verjetnostni račun in statistika), Jože Andrej Čibej, DZS Ljubjana, 1991
- ZBIRKA M: kombinatorika, verjetnostni račun in statistika, France Avsec, Aleksander Cokan, Ivan Pucelj, DZS Ljubljana, 1991
- OSNOVNI POJMI STATISTIKE, Aleksander Bajt, Univerza v Ljubljani (pravna fakulteta), 1997
- STATISTIKA, Anuška Ferligoj, Univerza v Ljubljani (FDV)
