FILTRI (sita)

Vsako kombinacijo pasivnih elementov (R,L in C) v povezavi z ali brez aktivnimi elementi (tranzistor, op. Ojačevalnik), pri uporabi v frekvenčnem prostoru imenujemo filtri. V splošnem filtre delimo na:
  1. Pasivni filtri, ki vsebujejo paralelno ali serijsko vezavo elementov R, L in C.
  2. Aktivni filtri, ki vsebujejo ojačevalni element tranzistor ali operacijski ojačevalnik in kombinacijo elementov R, L in C.

Na to kako se obnašajo v frekvenčnem območju ji delimo na:
  • nizkofrekvenčni ali nizko prepustni filtri

  • visokofrekvenčni ali visoko prepustni filtri

pasovno prepustni filter

pasovno zaporni filter

 

Posebna vrsta filtrov so kristalni ali keramični filtri, ki delujejo na osnovi piezo-efekta ali površinskih valov.
  1. kristal – prerez in slika

 

 

 

 

c) keramični filtri

d) filter na osnovi površinskih valov ( za MF pri TV)

Primeri vrste LC filtrov konstante K:

Nizko prepustni filtri:

G - filter

T – filter

p - filter

Visoko prepustni filtri:

 

 

Pasovni filtri:

 

 

R-C nizko prepustni filter

Zelo nizke frekvence!

Zelo visoke frekvence!

Pri nizkih frekvencah predstavlja kondenzator zelo veliko upornost, zato je vhodna napetost enaka izhodni. Pri visokih frekvenca se upornost kondenzatorja toliko zmanjša, da ta predstavlja kratek stik in izhodna napetost je enaka nič. Kjer bo izhodna napetost padla na Uizh = 0,707 Uvho oziroma R = XC , je mejna frekvenca, do katere frekvence filter prepušča.

Mejo filtra do kje prevaja in od kje ne prevaja določimo tako, da se od maksimalne izhodne napetosti, spustimo na vrednost 1 / Ö 2 ali na vrednost 0,707 Uizh. Na tej vrednosti je fazni zasuk vezja točno –450.

Razmerju izhodne in vhodne napetosti pravimo ojačanje, ki pa je pri idealnih pasivnih filtrih enako ena, če prevajajo.

...1 .....2

....3

Izračun izhodne napetosti: Mejna frekvenca:

....4 ....5 pri Xc=R

 

Razmerje med izhodno in vhodno napetostjo na filtru ali katerem koli elektronskem vezju, imenujemo ojačanje ali slabljenje. Če to opazujemo pri različnih frekvenca dobimo diagram, ki ga imenujemo prenosna karakteristika vezja.

Ker pri filtru opazujemo ravno obnašanje izhodne napetosti pri različnih frekvencah, bomo to najpogosteje prenosna karakteristika.

Amlitudni del (ojačanje) prenosne karakteristike in fazni del nam podaja BODE-jev diagram.

 

Risanje prenosne karakteristike elektronskih vezij v BODE-jevem diagramu

 

R-C nizko prepustni filter

Nizko prepustni filter, kot smo ga že spoznali, si bomo ogledali v BODE-jevem diagramu. Ker v njem potrebujemo ojačanje v dB si ga moramo preračunati z enačbo 6 in fazni kot z enačbo 7.

 

 

...6

....7

 

Za lažjo predstavitev diagrama si narišemo v asimptotah, ki jo predstavlja poenostavljena enačba:

 

...8 fm = fzg (zgornja mejna frekvenca)

 

Enačba (8) je poenostavljena enačba (6) tako, da nam predstavlja asimptote (to so premice, ki se dotikajo v eni točki krivulje in tako približno predstavljajo pravo krivuljo na določenem odseku).

Z asimptotami si bomo tako lahko predstavili celoten prenosni diagram brez podrobnega risanja krivulje.

Asimptota ojaèanja ali amplitude upada od mejne frekvence proti podroèju slabljenja z naklonom 20dB/dekado.

Fazni kot se spremeni v celotnem frekvenčnem področju za 90o pri idealnem RC filtru.

Fazni kot je tako pri nizko prepustnem filtru pri mejni frekvenci fzg natanko –45o.

Od te vrednosti dol in gor po frekvenčnem merilu pada z naklonom –45o/ dekado (asimptota upada od 0o pri nizkih frekvenca do –90o pri visokih frekvencah.

Več od te asimptote je ravna črta, ki pove, da se kot zasuče le za 90o.

Pri realnih filtrih je maksimalni kot zasuka okrog 60o zaradi izgub!

Prava krivulja odstopa od asimptot ob pregibih kot je vidno na naslednji sliki.

BODE-jev diagram za RC-nizko prepustni filter:

Pravila risanja BODE-jevega diagrama z asimptotami:

 

R-L nizko prepustni filter

Mejna frekvenca: = fzg

 

 

R-C visoko prepustni filter

Ker kondenzator enosmernega toka ne prepušča bo filter začel prevajati le od neke frekvence naprej. Pri zelo visokih frekvenca predstavlja kondenzator kratek stik in takrat je vsa vhodna napetost tudi na izhodu.

 

Ker filter začne prevajati pri neki višji frekvenci, imenujemo to mejno frekvenco spodnja mejna frekvenca.

 

Izračun:

..9 ...10 ...11

 

....12

 

Izračun ojačanja filtra v dB:

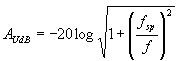...13

 

oziroma poenostavljen izračun ojačanja in faznega kota, če bomo risali diagram z asimptotami:

 

/ f << fm ....14 in fazni kot: ...15

 

S pomočjo teh dveh enačb (14 in 15) si lahko narišemo BODEjev diagram za visoko prepustni RC filter.

BODEjev diagram za visoko prepustni filter.

 

BODEjev diagram narisan s simulacijskim programom: R=1k, C=1uF

 

 

R-L visoko prepustni filter

 

Po karakteristikah (prenosni diagram-BODE) se RL filter enako obnaša kot RC le, da je tuljavo težje narediti in še večja je kot kondenzator.

Pasovni R-C filtri

S kombinacijo nizko prepustnega in visoko prepustnega filtra lahko dobimo pasovno prepustni ali pasovno zaporni filter.

  1. pasovno prepustni

b) pasovno zaporni

S kombinacijo R,L in C elementov lahko dobimo zelo kvalitetne prepustne filtre oziroma dobimo nihajne kroge, ki smo jih že obravnavali.

 

Aktivni filtri

Pasivni elementi v kombinacijah RC, RL in LC omogočajo izdelavo nizko in visoko prepustnih ter pasovnih filtrov. LC filtri niso primerni za nizke frekvence zaradi velikih tuljav. Za nizke frekvence so zato primerni RC kombinacije, ki pa imajo slabost majhno kvaliteto. To kvaliteto lahko popravimo, če dodamo operacijski ojačevalnik. S tem smo dobili aktivni filter.(glej dodatek!)

 

 

Nizko prepustni filter

 

 

 

Visoko prepustni filter